Appendix - Part F

Keywords: UFO, unidentified flying objects, Bible, flying saucers, prophecy, Paleo-SETI, ancient astronauts, Erich von Däniken, Josef F. Blumrich, Zecharia Sitchin, Ezekiel, biblical prophecy, spacecraft, spaceship, NASA, Roswell, aircraft, propellant, extraterrestrial hypothesis, Jacques Vallee, interdimensional hypothesis, Project Blue Book, Condon Report, ancient history, Jesus, Judaism, Christianity, Middle East, end times, engines, rockets, helicopters, space travel, aliens, abductions, alien abductions, crop circles, extraterrestrials, astronomy, economics, biology, Venus, Mars, Jupiter, Saturn, Space Shuttle, Apollo, stars, planets, solar system, scriptures, design, fuel tank, aerodynamics, fuels, hydrogen, oxygen, wheels

Appendix

    (a) Flight conditions

    Lift-off Weight W₀: This weight will be considered over a range of 10,000-100,000 kilograms (22,000 - 220,000 lbs).  [p.160]

    Specific Impulse I_sp: As already mentioned, this figure indicates how many kilograms (or lbs) of thrust will be produced for each kilogram (or lb) of propellant consumed per second. Besides that direct dependence on the type of propellant, this figure also is influenced by the engine design and by the environment, that is, it depends on whether it operates in the atmosphere or in a vacuum. Theoretical investigations have shown that this value can by far exceed the now achievable maximum of about 800-900 sec. For that reason, a range of 1,000-10,000 sec was considered in the analysis.

    Velocity v: This includes several component velocities, the most significant of which is determined by the orbital altitude. This amount results from the simple requirement that the centrifugal force due to the circular motion must equal the weight of the vehicle if that body is to stay in orbit. The additional velocities result from the following considerations: In order to achieve the circular orbit, the vehicle must pass through the atmosphere that means it has to overcome aerodynamic drag; it also must overcome the gravitational attraction of the earth; and finally, its flight path must be changed from the ascent trajectory into the circular orbit. All these efforts require energy which can be expressed in velocity increases and which, in that form, is used in the basic formula. In our case the resultant total velocity for the expected orbital altitude of about 400 kilometers (220 nautical miles/249 miles) is about 9300 meters per second (30,500 ft/sec).

    The first result is obtained by using these values in the basic formula it is represented in Fig. 23 by the curves marked W₀.

    (b) Structural weights

    Introduction: The total weight can be subdivided as follows.

Structure	W1	Main body
	W2	Main engine
	W3	Radiation shield
	W4	Helicopter drive
	W5	Rotor
	W6	Landing gear
	W7	Command capsule
Propellant	W8	Braking and control
	W9	Ascent flight
Landing	W10	Touchdown weight

The structural weight of a given vehicle is constant; the propellant weight changes with the propellant consumption during flight. Since the total weight—the sum of these two major weight groups—determines the dimensions and therefore the weight of the structure, its magnitude must be determined for various phases of the operation.

    Weight changes during the operation: We selected liftoff weight W₀ for the return flight into orbit as starting and reference point for all weight determinations. Using the above list we obtain the following expression: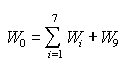

    In this expression we have intentionally neglected the small amount of propellant necessary to bring the spacecraft to its mothership after it has reached orbit. Next, we obtain the simple equation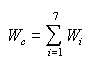

    The propellant weight necessary for the return flight can then be found by introducing those values that were determined by the flight conditions in part (a) above:

    As stated above, this term gives us the amount of propellant necessary for the return flight into orbit. That amount is not sufficient to size the propellant tank, however. For that purpose it is necessary to include the amount of propellant required for the braking during descent. Finally, there is also the propellant for the control rockets on board. Because of their relative insignificance, the two latter quantities are combined and estimated to amount to about 10 percent of W₉. The propellant tank will then be sized for the amount

    This simplification results in an insignificant oversizing of the propellant tank. Since the latter, in turn, determines the dimensions of the main body, that body also is influenced the same way. The respective weights will therefore be slightly higher than they would be as a result of a more accurate analysis.

    So much for the weight W₀ for the return flight. The weight at touchdown after descent from orbit, and the weight that is to be lifted by the helicopters for the terrestrial flights, is higher by the amount of the control rocket propellant because very little of it has been consumed at that moment. This amount, however, cannot be determined at all, but it is very small. Given the uncertainty of estimates here, it is much simpler to use higher factors in the weight determination of the respective structures than to try to assess small weight differences. Consequently, we will equate the touchdown weight as well as the weight for the terrestrial flights to the lift-off weight, and we can say:

    The influence of technology: Technology is changing constantly. Its changes parallel our penetration of the laws of nature and our ability to make use of them. On the one hand, therefore, all technological development means genuine progress while, on the other hand, it is dependent on time.

    With the very broad spectrum of influences that make a technical product and achievement possible, the available materials and their properties are of particular significance. They determine to a great extent whether an idea can be implemented at a given point in time. Beyond that, they determine, in combination with the abilities of the engineers in design and fabrication, the weight of a structure. For that reason, there exists a time dependence of the structural weights which, in general, will decrease with progressing development. We are therefore entitled to consider the same tendency also for the weight estimates performed here.

    The weight estimates are made in two steps. The first is the determination of weights as they can be achieved with our present state of the art; the second is the extrapolation into the future possibilities. The latter was again subdivided into two groups: one assuming a relatively modest amount of progress, and another accepting the possibility of a substantial improvement. That double extrapolation, which we will call Technology 1 and Technology 2 (abbreviated T₁ and T₂) will be used to gain insight into the length of time separating us from the realization of those structures. As far as possible, I have made use of existing information for the first step, although some assumptions on my part were unavoidable. As far as the extrapolations are concerned, they are, of course, never objective; just as in any other field, there is no sure and undebatable way to predict the future. The figures and ranges used were selected with great care, however, and by and large I believe them to be conservative.  [p.164]

    Individual weights