Appendix - Part I

Keywords: UFO, unidentified flying objects, Bible, flying saucers, prophecy, Paleo-SETI, ancient astronauts, Erich von Däniken, Josef F. Blumrich, Zecharia Sitchin, Ezekiel, biblical prophecy, spacecraft, spaceship, NASA, Roswell, aircraft, propellant, extraterrestrial hypothesis, Jacques Vallee, interdimensional hypothesis, Project Blue Book, Condon Report, ancient history, Jesus, Judaism, Christianity, Middle East, end times, engines, rockets, helicopters, space travel, aliens, abductions, alien abductions, crop circles, extraterrestrials, astronomy, economics, biology, Venus, Mars, Jupiter, Saturn, Space Shuttle, Apollo, stars, planets, solar system, scriptures, design, fuel tank, aerodynamics, fuels, hydrogen, oxygen, wheels

Appendix

    3. Results

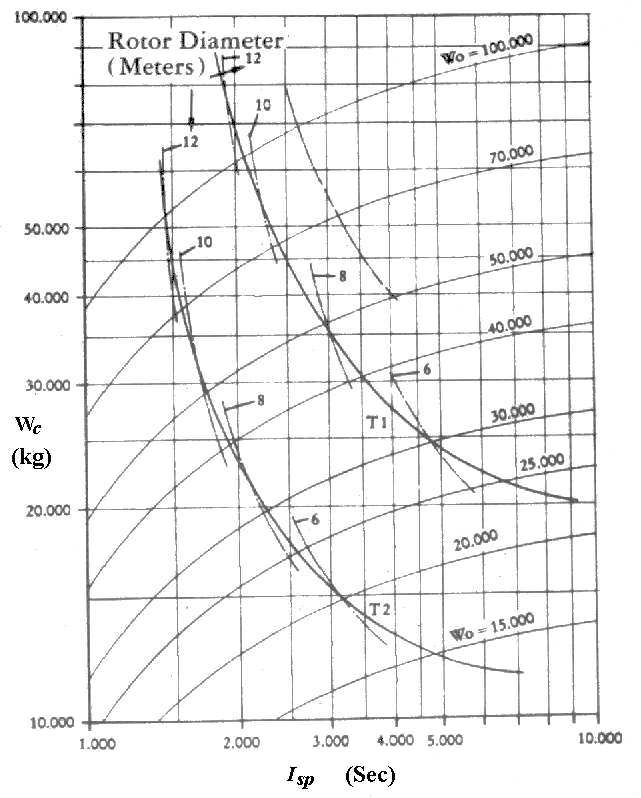Figure 23 Result of the analysis

    The calculations that have to be carried out are not difficult although they are somewhat time-consuming. Their results are shown in Fig. 23. The curves marked W₀ are the result of the first part of our analysis (see p. 160). The curves marked T₁ and T₂ are the final result of the superposition described there. It should be mentioned that in determining weights W₂ and W₃ from Figs. 20 and 21, the amount of thrust was set equal to 1.25W₀.  [p.171]

    Expressing in it general terms, we can say that Fig. 23 shows the weight reductions achievable with increasing specific impulse. The enormous importance of the development of engines with high specific impulse can hardly be demonstrated more impressively. We also see in this figure the very steep weight increase in the low I_sp range. It shows us clearly that even the extremely high level of technology, as it is expressed by the T₂ curve, does not make such a vehicle feasible with engines of today's technology, as has already been pointed out (page 25).

    The chart shows short lengths of curves indicating various rotor diameters; the points of intersection of these curves with the main curves (T₁ and T₂) indicate the maximum rotor diameter that is geometrically possible at the respective weights and dimensions. We know from Fig. 22 that the maximum rotor diameter can be about 62% of the diameter of the main body, and we can see now that the latter will vary between about 65 feet and 17 feet over the range investigated here.

    Considering the number of assumptions made, it is necessary to determine the sensitivity of the result to possible errors in the weight estimates. The investigation of the impact of a weight increase will be conducted differently in our study than in current actual cases. In the latter we are always working near the upper limits of available I_sp values; any weight increase will therefore always result in a performance loss of the vehicle—in whatever form that may be expressed. In our present investigation, however, the I_sp value is not really limited. Consequently, an increase of the structural weight does not entail an increase of lift-off weight, because it can be balanced by a reduction of the propellant weight. The reduced amount of propellant, in turn, will be compensated for by an engine with a higher specific impulse.

    The dashed line in Fig. 23 shows the result of a 10 percent weight increase for part of the T₁ curve. Such a weight increase can either be shared proportionately by all structural systems or can occur in one group only. We see clearly that even considerable weight corrections will not basically change the results.

    In order to find an answer to the question where in the chart we have to look for the spacecraft seen by Ezekiel, it is now only necessary to consider the general relationship of curves T₁ and T₂ to the I_sp values. As we have seen, T₁ corresponds to a moderate technical development beyond our own current level, while T₂ postulates a very considerable one. With regard to the specific impulse, its higher values belong quite obviously to a higher level of engine development. It may well be that the level of development is not the same in all fields; in terms of time, such differences between related technologies can only amount to years but certainly not to decades. In order to explain this, let us look at one example: The present high level of the medical sciences is completely unthinkable at the level of electronics and materials sciences of, say, 1940. There are analogous situations in every field. Applied to our graph (Fig. 23), that means generally a connection of low I_sp with T₁ and of high I_sp with T₂. Graphically illustrated, the actual course of development begins with T_l and low I_sp, and approaches T₂ with progressing development.

    Beginning with low I_sp values, we find ourselves in the range of relatively large diameters as a result of the above considerations; we find large helicopters and main bodies, and we find the general vehicle characteristics as expressed in Figs. 1 and 2. For an investigation of the other end of the spectrum we take an I_sp value of about 7000 seconds. Even if we assume that the technological development has not completely reached the curve T₂, we find lift-off weights W₀ of 15,000 kg (33,000 lbs) or less. We notice furthermore that the reduction of rotor diameters leads to unrealistic helicopters, and that their power plants assume a disproportionately high percentage of the total weight. A combination of these findings with the fact that the main engine now is not only small, but also is based on a different principle than the one postulated so far, results in the surprising conclusion that the helicopters are not necessary any more. Since the weight of the helicopters and their power plant has become uneconomical, it can now be replaced by respective amounts of propellant, which becomes available for terrestrial flights. Such flights are then time-limited, of course, but that will be acceptable if a propellant is selected that can relatively easily be replenished on earth.

    The exchange of the weight of the helicopters and their power plants for propellant weight and volume requires a larger main tank. . . .  [p.173]